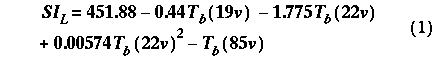
Volcanic ash clouds are a significant hazard to aviation [Casadevall, 1994], and there is a considerable effort being expended to mitigate this hazard. Volcanic clouds are remotely sensed by many ground-based and satellite sensors. Ground-based radar systems have been shown to be useful during and for up to 30 minutes following volcanic eruptions [Harris and Rose, 1983; Rose et al., 1995a], however most volcanoes are out of range of modern radar systems. A variety of satellite-based ultraviolet and infrared sensors are used to track volcanic clouds for several days as they disperse in the atmosphere [Krueger, 1983; Schneider and Rose, 1995]. Infrared sensors, such as the Advanced Very High Resolution Radiometer (AVHRR), have some important limitations in the remote sensing of volcanic clouds. Near the volcanic vent, many volcanic clouds are opaque in the infrared region. This results in difficulties in the detection of volcanic clouds (since they look similar to meteorological clouds in infrared images) and in determining the particle size distribution and mass of volcanic clouds [Wen and Rose, 1994]. The SSM/I sensor can be used to estimate particle size and mass of the volcanic clouds that are opaque to infrared sensors and out of range of ground-based radar systems. The SSM/I instrument can also be used to estimate the ashfall deposits where ground based reconstruction is difficult./p>
The SSM/I is a seven-channel, linearly-polarized, passive microwave radiometric system which measures radiation at 19.35, 22.235, 37.l0 and 85.5 GHz [Hollinger et al., 1987]. Note that there is no 22.235 GHz horizontal polarized channel. The instrument is a conically scanning radiometer which scans a 102 degree segment at an earth incident angle of 53 degrees (see figure 1). The SSM/I instrument was first aboard the F8 Defense Meteorological Satellite Program (DMSP) satellite which was launched in July 1987. The 85 GHz channels failed within the first two years of operation, resulting in the F8 DMSP satellite not being very useful for the study of volcanic clouds. There are also SSM/I instruments aboard the F10 and F11 DMSP satellites, which were launched in December 1990 and November 1991, respectively. The sampling rate of the SSM/I instrument results in a pixel size of 12.5 x 12.5 km for the 85 GHz channels and 25 x 25 km for the 19, 22, and 37 GHz channels. The current Marshall Space Flight Center (MSFC) conversion algorithms are used to convert National Environmental Satellite, Data, and Information Service (NESDIS) level 1b sensor counts [Lee, 1993] to antenna temperatures and then brightness temperatures. For a more detailed description of the SSM/I instrument and how the brightness temperature data are computed, see the Users Guide to Special Sensor Microwave Imager (SSM/I) Data which is available from the Marshall Space Flight Center Distributed Active Archive Center.
The SSM/I instrument is designed to aid in the forecasting of weather for the Department of Defense. Passive microwave data have also been applied to land-surface-type classification [Neale et al., 1990], snow and sea ice studies [Kunzi et al., 1976], and precipitation estimates [Wilheit, 1986]. Currently, researchers are using SSM/I data to study the global hydrological cycle [Ferraro et al., 1994a]. In this paper, I exploit the knowledge obtained from the study of meteorological clouds using SSM/I data and apply these methods to volcanic clouds.
The remote sensing of meteorological clouds forms a good basis for the study of volcanic clouds because of the characteristics they share. Many meteorological clouds contain ice particles which behave similarly to possible ice coated ash particles in volcanic clouds [Rose et al., 1995b]. The sizes of the ice particles in meteorological clouds are similar to the large (mm sized) silicate ash particles in volcanic clouds. Due to these similarities, it is reasonable to assume that volcanic clouds can be studied using the methods developed for the study of meteorological clouds. In this paper, we exploit the knowledge obtained from the study of meteorological clouds using SSM/I data and apply these methods to volcanic clouds.
The SSM/I sensor has not been used before in the remote sensing of volcanic clouds but based on its previous application to meteorological studies, it has the potential for providing information about particle sizes and mass during and shortly after eruptions. The SSM/I instrument uses wavelengths between that of radar and infrared systems and is particularly useful for sensing particles ranging in radius from 0.1 to 20 mm. We present results on a study of SSM/I data collected during the August 19, 1992 eruption of Mount Spurr, Alaska.
The SSM/I data archive was searched for possible detection of the recent, relatively large eruptions of Mount Spurr, Lascar, Klyuchevskoi, and Rabaul. There are several reasons why not all volcanic clouds are observed by the SSM/I instruments. (1) the SSM/I instrument has a 1400 km swath, which results in a single satellite only observing about 60% of the Earth in 24 hours. The inter-swath gaps vary from day to day resulting in changes in the area observed; (2) there are sometimes data gaps within the SSM/I orbits; and (3) it may not be possible for microwaves to detect volcanic clouds older than about one hour because millimeter sized particles fall out quickly [Rose et al., 1995a].
This paper focuses on the volcanic cloud emitted from the August 19, 1992 Crater Peak/Spurr eruption. The reasons for selecting this volcanic cloud for study is because of the satisfactory SSM/I image (see figure 2), along with complementary ground-based C-band radar and satellite-based AVHRR data. The SSM/I image captured the volcanic cloud during the middle of the eruption which lasted between 01:42 and 05:10 GMT [Rose et al., 1995a]. Due to the shorter wavelength, which is sensitive to smaller particles, and the better spatial resolution, the 85 GHz channel is best for detecting volcanic clouds.
When the SSM/I brightness temperature data were imported into our Terascan (TM) software package, the data were found to suffer from navigational errors. These errors caused the land/water boundaries to be incorrect when overlaying the coast on an image. Therefore, each SSM/I image is adjusted until the land/water boundaries of the map overlay coincide visually with the land/water boundaries of the SSM/I data. The selective nature of this process results in navigational error of as much as 5-10 km. Ferraro and Marks [1995] reported having similar (10 km) navigational errors with SSM/I data.
The SSM/I instrument has a 53 degree incidence angle and the Crater Peak/Spurr volcanic cloud that we observed had a cloud top height of about 14 km [Rose et al., 1995a]. This results in the volcanic cloud being offset in relation to its true map position. Using the satellite incident angle and the height of the cloud, the volcanic cloud position can be adjusted. The adjusted position of the SSM/I volcanic cloud can then be compared with that observed by radar and AVHRR (see figure 3). The volcanic cloud area detected by the SSM/I instrument is larger than the area detected by C-band radar, but smaller than the area detected by AVHRR. This is due to the fact that when the majority of the particles in the volcanic cloud are smaller than a minimum particle size, the instruments no longer detects the volcanic cloud. The minimum particle size detectable by an instrument is hard to quantify precisely because of the combined effects of the particle size distribution, the single particle cross-section, the different shapes of particles, and the specifications of the instrument.
In this section, the August 19, 1992 Crater Peak/Spurr volcanic cloud is analyzed by adapting methods developed for the study of meteorological clouds. By imploying these methods, the similarities and differences between volcanic clouds and meteorological clouds are developed.
SSM/I scenes can be classified into two components, absorbing surfaces and scatterers [Grody, 1991]. Absorbing surfaces (water, melting snow, vegetation) have brightness temperatures that increase with frequency. This occurs because of the absorption effects of water in these materials. In contrast, scatterers (dry snow cover, desert sand, precipitation) have brightness temperatures that decrease with increasing frequency. Scattering areas on an SSM/I image occur where radiation have been emitted and then scattered by particles before being detected by the SSM/I sensor. In contrast, absorbing areas occur where radiation is emitted from a surface and not scattered before being detected by the SSM/I sensor.
Procedures have been developed and refined that use SSM/I data to compute a scattering index for the 85 GHz vertical polarization channel [Grody, 1991; Flore and Grody, 1992; Weng et al., 1994]. The scattering index is computed by using the low frequency channels (19 and 22 GHz) to estimate the 85 GHz brightness temperature for non-scattering conditions and then substracting the observed 85 GHz brightness temperature. The stronger the area scatters radiation, the higher the scattering index. The scattering index for the August 19, 1992 Crater Peak/Spurr volcanic cloud (see figure 4) was computed by using the most recent land surface scattering formula [Ferraro et al., 1994b]:
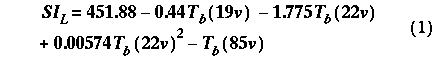
where Tb is the SSM/I brightness temperature for the vertical polarized 19, 22 and 85 GHz channels. The image of the scattering index shows that the volcanic cloud is a strong scatterer of radiation at a frequency of 85 GHz. A minimum scattering index value of between 5 K and 10 K works well to define the edge of the volcanic cloud. A threshold value of 5 K removes most of the background, whereas a threshold value of 10 K eliminates any false signatures (non-volcanic cloud pixels). In global precipitation classifications, a threshold value of 10 K is used, however, for regional applications the threshold can be reduced [Ferraro et al., 1994b]. By using the scattering index with a minimum threshold, the edge of the volcanic cloud can be determined systematically instead of arbitrarily choosing the edge based on the 85 GHz channel.
In addition to the volcanic cloud, figure 4, also shows scattering due to snow cover and precipitation. Once an area has been identified as a scatterer, the equations, Tb(22v)>264 and Tb(22v)>175+0.49Tb(85v), are used to distinguish whether scattering is due to precipitation or snow cover [Ferraro et al., 1994b]. Dry snow cover acts as a scatterer because it contains small particles separated by air spaces. These small particles scatter the radiation emitted from the ground below. Precipitation clouds, which contain ice particles, are scatterers because the ice particles scatter radiation emitted by the Earth's surface. A plot of the 85V vs 22V GHz channel for the August 19, 1992 Crater Peak/Spurr volcanic cloud is displayed in figure 5, which shows that the volcanic cloud straddles the empirical boundary between precipitation and snow cover. In general, this makes it difficult to distinguish volcanic clouds from either snow cover or precipation. However, for large volcanic eruptions in areas without snow cover, it seems likely that volcanic clouds could be distinguished from meteorological clouds. A good candidate for future study is the 1991 eruption of Mount Pinatubo, Philippines
It is important to determine the Earth's surface brightness temperature beneath the volcanic cloud to be able to calculate the particle size distribution and mass of the volcanic cloud. One possible method to estimate the underlying brightness temperature is to use the brightness temperature of the pixels surrounding the volcanic cloud. Due mainly to changes in emissivity, the pixels surrounding the volcanic cloud have brightness temperatures that vary by five degrees. Another method for estimating the underlying brightness temperature is to use the brightness temperature 24 hours preceding the eruption. This assumes that the surface emissivity and temperature do not vary greatly between the two observations. To test this assumption, several different days were compared to see how the brightness temperature changed in 24 hours. For our area of interest and time of year, it was found that the brightness temperature changes no more than one degree. Therefore, it seems that this assumption is reasonable and gives a smaller error than using the brightness temperature of the surrounding pixels. This method also has the advantage of having variable brightness temperatures underlying the volcanic cloud, which takes into account the changes in emissivity. Figure 6 compares the frequency dependence of brightness temperature for volcanic clouds, dry snow and heavy rain. Also shown are the SSM/I brightness temperatures of the Mount Spurr area 24 hours preceding the eruption.
The low brightness temperatures that are observed for the volcanic cloud (see figure 2) are the result of scattering of earth-emitted radiation by particles within the volcanic cloud. The scattered intensity for a single particle depends strongly on the ratio of the particle size to the wavelength of the incident wave. This ratio defines two major types of scattering, Rayleigh and Mie scattering. If the incident wavelength is less than 1/10 of the particle size, the resulting scattering is defined as Rayleigh scattering. Mie scattering occurs when the incident wavelength is on the order of the particle size. McCartney [1976] and van de Hulst [1981] give in-depth discussions on the scattering of radiation by cloud particles.
Figure 7 shows the scattering efficiency factors for ice and ash particles. Note that the differences in the magnitude of efficiency factors are due to the differences in the refractive index between ice and ash particles. The efficiency factor is the ratio of the particle's cross section to it's geometrical cross section. The total energy scattered in all directions is equal to the energy of the incident wave falling on the area of the particle's scattering cross section. For the Rayleigh scattering region, the efficiency factor is relatively small which results in a small effect on the brightness temperature. The scattering efficiency factor does not become large until you enter the Mie region. The Mie region is from the upper end of the Rayleigh region until there is a constant efficiency factor. When two channels have the same scattering efficiency factor, the brightness temperature that they observe will be the same since they scatter earth-emitted radiation in a similar fashion. This is possible in band 4 and band 5 of the AVHRR observing a volcanic cloud with large (mm sided) particles [Lin and Coakley, 1993].
The particles in the volcanic cloud have a major effect on the brightness temperature observed by the SSM/I instrument. The SSM/I instrument detects a varying decrease in surface brightness temperature. For these reasons, the particle size in the volcanic cloud detected by the SSM/I instrument is in the Mie region where particles range in radius from about 0.1 to 20 mm.
Volcanic clouds contain a range of particle sizes, which can be described by a particle size distribution. To determining the mean value of the particles size distribution and the mass of a volcanic cloud that is observed by the SSM/I instrument a simple radiative transfer model is developed. A more complex radiative transfer model would include emission by particles within the volcanic cloud [Lin and Coakley, 1993; Prata, 1989].
By assuming that there is little absorption/emission by the cloud, the emerging brightness temperature (Tb) observed by the SSM/I satellite can be approximated by [Grody and Basist, 1994]:
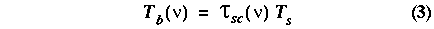
where t is the transmittance and Ts is the surface brightness temperature. Neglecting multiple scattering, the transmittance is:
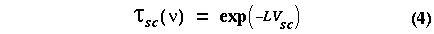
where L is the thickness of the cloud and V is the volume scattering coefficient. The volume scattering coefficient is given by:
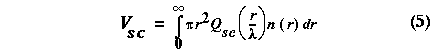
where n(r) is the particle distribution, lamda is the wavelength, and r is the particle radius. The scattering efficiency factor (Qsc) for ice and ash particles are plotted in figure 7. The scattering efficiency factor is computed using Mie theory [Barber and Hill, 1990]. Due to the similarities between ice and ash scattering efficiency factors, it is difficult to distinguish ice from ash particles. As a consequence, it is difficult to determine if the SSM/I instrument is detecting ash particles or ice coated particles without using supplementary data.
Based on aircraft sampling of volcanic clouds, a lognormal distribution is considered to be the most appropriate particle size distribution for volcanic clouds [Farlow et al., 1981]. The normalized lognormal distribution has the following form:
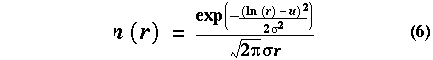
where r is the particle radius, u is the mean, and sigma is the standard deviation. Based on volcanic cloud measurements, a standard deviation of 0.74 is used for the lognormal distribution [Hobbs et al., 1991; Wen and Rose, 1994]. The volume scattering coefficient can therefore be computed for any wavelength if a mean value is chosen for the particle size distribution. The transmittance of the cloud can be calculated by using observation of the volcanic cloud brightness temperature (Tb) and the surface brightness temperature (Ts). By combining observations from two different channels, the following equation can be written:
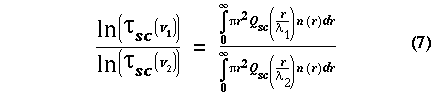
In the above equation, the frequencies and wavelengths are chosen to correspond to two of the channels of the SSM/I instrument. By selecting two channels, the left side of the equation is determined by SSM/I observation of the volcanic cloud. On the right side, a lognormal distribution is used with a standard deviation of 0.74. The mean of the particle distribution is found when the right side of the equation equals the left.
Care must be taken to use channels where the assumption of scattering dominance is valid. One method of determining if scattering is dominant is to look at the opaque region of the volcanic cloud as observed by AVHRR. The opaque region of the August 19, 1992 Crater Peak/Spurr volcanic cloud has a brightness temperature of 214 K in the infrared region, whereas the SSM/I 85 GHz brightness temperature is 211 K (see figure 6). Assuming that emissivity is relatively constant with frequency, a 85 GHz brightness temperature near 214 K would be emission from the volcanic cloud surface and not scattering of earth-emitted radiation. Therefore, to determine the mean of the particle distribution, the 37 and 19 GHz channels were used. The index of refraction value for ash particles in the Crater Peak/Spurr eruption [Adams et al., 1995] were used in computing the scattering efficiency factor. The mean radius was found to be 0.9 mm for a lognormal particle size distribution.
A mean particle size of 0.9 mm seems reasonable when considering that C-band radar has the most intense reflection for particles ranging in radius from 1-10 mm [Rose et al., 1995a]. The size of the SSM/I sensed volcanic cloud is larger than the size of the volcanic cloud detected by C-band radar, therefore the size of the particles that the SSM/I detects should be smaller. For the August 19, 1992 Crater Peak/Spurr eruption, theoretical calculations indicate that spherical ash particles with a radius of 0.5 mm fall out within about half an hour [Rose et al., 1995a]. Therefore, for volcanic eruptions similar in size to the August 19, 1992 Crater Peak/Spurr eruption, the SSM/I instrument can only detect the volcanic cloud for a little more than about half an hour after the end of an eruption.
Based on the SSM/I data, two different methods for estimating the total volume and mass of ash in an eruption are developed. The first method is based on the simple theoretical radiative transfer model outlined in the previous section. The second is an empirical method which relates the scattering index to an ashfall rate. The empirical method comes close to estimating the mass determined by field measurements of the actual ash deposits [Neal et al., 1995]. Table 1 contains estimates of the total volume and mass for the August 19, 1992 Crater Peak/Spurr volcanic cloud based on these methods along with an estimate based on ground sampling of the ashfall blanket.
Once the mean value of the lognormal distribution is determined, it is possible to calculate the mass of the volcanic cloud using equation 3 if we assume that the particle size distribution is constant for the entire volcanic cloud and that the decrease in transmissivity is due only to the volcanic cloud. This method of calculating the mass of the volcanic cloud only estimates the amount of ash in the air at the time of observation. Based on theoretical calculations for the August 19, 1992 Crater Peak/Spurr eruption, spherical ash particles with a diameter of one millimeter, would fallout within a half hour [Rose et al., 1995a]. Therefore, to estimate the total mass, the instantaneous mass of the cloud would have to be multiplied by a factor of seven or more for the August 19, 1992 Crater Peak/Spurr eruption which lasted for 3.5 hours [Rose et al., 1995a]. This assumes that the ash emission rate is constant.
The scattering index can be used to estimate the rainfall rate once an area has been classified as precipitation. The current empirical equation used to calculate the rainfall rate (mm/hr) from the scattering index (SI) over land surfaces is given as follows; [Ferraro and Marks, 1995].
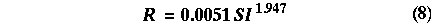
A similar empirical relationship could be developed to relate the scattering index to an ashfall rate. For the development of such a relationship however, it would be necessary to have several SSM/I observations along with "ground truth" information about the ashfall rate. These types of data are not available at present, therefore we decided instead to use dielectric data to modify the rainfall rate equation to give an estimate of the ashfall rate. The radar return from an ash particle is less than that from a water particle. A correction factor (alpha) can be computed due to the difference index of refraction of water and ash. The refractive index factors for ash and water are 0.39 and 0.93, respectively [Rose and Kostinski, 1991; Adams et al., 1995]. Based only on the different refractive index factors, the correction factor for radar reflectivity would be 0.42. Assuming that the change in refractive index has a similar effect on the scattering index as on radar returns, the alpha correction factor can be applied to equation 7 to give an ashfall rate.
Support for the use of this alpha correction factor is found when it is applied to calculating radar reflectivity of the volcanic cloud based on the scattering index. For stratiform rain the following empirical equation relates the reflectivity factor (Z) to the rainfall rate [Skolnik, 1990].
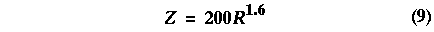
By combining this equation and equation 8, the radar reflectivity for a meteorological cloud can be calculated based on the SSM/I scattering index. Table 2 compares this value to that of the observed reflectivity and the reflectivity using the alpha correction factor. The reflectivity based on stratiform rain is higher than that observed by radar, whereas the corrected reflectivity agrees better with the ground-based C-band radar observation.
Figure 8 shows the results of using the modified rainfall relationship. The eruption rate was assumed to be constant and the eruption duration is assumed to be 3.5 hours. Once the ash thickness is determined, the areal extent can be used to calculate the total volume of the eruption. For the Crater Peak/Spurr eruption a density of 2600 kg/m^3 can be assumed [Neal et al., 1995] and the total mass of the volcanic cloud can be calculated.
There are several reasons why methods outlined in this paper may incorrectly estimate the mass of the volcanic cloud: (1) The center of the volcanic cloud is opaque at 85 GHz, which means that the assumption that the main effect is due to scattering is not valid; (2) the poor spatial resolution of the SSM/I instrument results in mixed pixel problems. The pixels at the edge of the volcanic cloud are only fractionally composed of the volcanic cloud which results in higher brightness temperatures than if they were completely filled; (3) the ash particles are assumed to be spherical which is incorrect [Heiken and Wohletz, 1985]; (4) some of the mass of the volcanic cloud is contained in particles which are too small for the SSM/I instrument to detect; (5) the ash emission rate may not be constant. The theoretical method also has the problem of determining the fallout time of ash particles, which is necessary to be able to determined the total mass of the volcanic cloud from a single observation. Determining the fallout time is difficult since there is a distribution of particle sizes which results in a distribution of particle fallout times.
However, the largest potential source of errors in the mass calculation methods is due to the determination of the areal extend of the volcanic cloud. A microwave detector with a higher spatial resolution or a deconvolution scheme [Farrar et al., 1994] can be used to reduce this error. Many other improvements can be made to the basic models presented in this paper for determining particle size and mass of volcanic clouds, however the poor spatial resolution and instantaneous view will still be major difficulties to overcome.
Currently, meteorologists are developing and deploying new satellite sensors to extent their data coverage in both time and space to enable study of the global hydrological cycle. Many of these sensors will improve our ability to study volcanic clouds in the microwave region. The Tropical Rainfall Measuring Mission (TRMM) satellite will have a microwave imager and precipitation radar [Weinman et al., 1994]. The microwave imager is similar to the SSM/I with an improved horizontal resolution of 5 km. These sensors and other future satellites will improve our ability to estimate mass and ash fallout of volcanic clouds. Modern ground-based radar have some advantages over satellite-based microwave sensors, however most volcanoes are not in the range of ground-based radars. By using ground-based radar to calibrate and verify microwave sensors, the study of volcanic clouds in the microwave region can be conducted on a global scale.
In the future, microwave satellite detectors could be used in real time detection of volcanic clouds. Both the size and trajectory of volcanic clouds are very important to hazard mitigation of volcanic eruptions. Seismic data can be used to determine the size of eruptions, however seismic data are not always available. Once a volcanic cloud is detected, it's trajectory, along with an estimate of the eruption magnitude and ash fallout, could be used in the warning of aircraft and the nearby population. By including the SSM/I sensor, along with other satellite sensors, the chance of early satellite detection of volcanic clouds is improved.
In the future, microwave satellite detectors could be used in real time detection of volcanic clouds. Once a volcanic cloud is detected, it's trajectory, along with an estimate of the eruption magnitude and ash fallout, could be used in the warning of aircraft and people. The size and trajectory of volcanic clouds are very important to hazard mitigation of volcanic eruptions. Seismic data can be used to determining the size of eruptions, however seismic data is not always available. By including the SSM/I sensor, along with other satellite sensors, the chance of early satellite detection of volcanic clouds is improved.
If SSM/I data can be collected during the eruption or within 30 minutes of it's termination, it provides information similar to ground-based meteorological systems, which are rarely in the range of active volcanoes. From the SSM/I data a scattering index can be quickly computed and a threshold of 5-10 K can be used to define the volcanic cloud. SSM/I data can be used to estimate the particle size distribution and mass of volcanic clouds. The trajectory and shape of the volcanic cloud can be determined if corrections for navigational errors and incidence angle are made. Also, SSM/I data can forecast an estimate of ash fallout. In the case of the August 19, 1992 Crater Peak/Spurr, the SSM/I data estimated the ash mass to be 0.13-3.0 x 10^10 kg, about 4-84% of the mass determined from the field measurements of the ashfall blanket. SSM/I can provide useful information for volcanological use as well as hazard mitigation.